| 失效链接处理 |
|
二叉树的建立及其基本操作 PDF 下载
本站整理下载:
相关截图:
主要内容:
一、实验目的
掌握二叉树的链式存储结构的建立方法和对二叉树的各种操作算法。利用二叉树的基本操作,构造哈夫曼树。
二、实验内容1
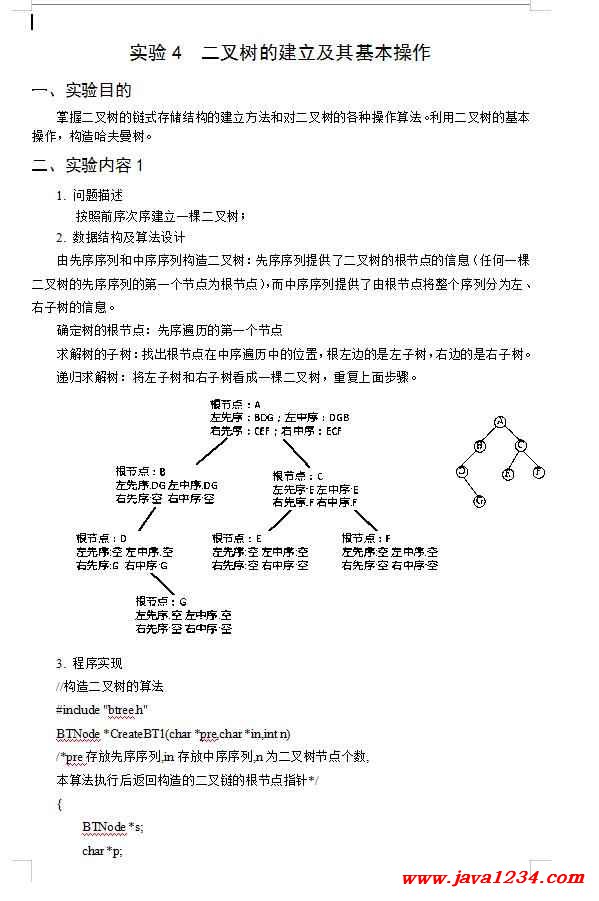
1. 问题描述
按照前序次序建立一棵二叉树;
2. 数据结构及算法设计
由先序序列和中序序列构造二叉树:先序序列提供了二叉树的根节点的信息(任何一棵二叉树的先序序列的第一个节点为根节点),而中序序列提供了由根节点将整个序列分为左、右子树的信息。
确定树的根节点:先序遍历的第一个节点
求解树的子树:找出根节点在中序遍历中的位置,根左边的是左子树,右边的是右子树。
递归求解树:将左子树和右子树看成一棵二叉树,重复上面步骤。
3. 程序实现
//构造二叉树的算法
#include "btree.h"
BTNode *CreateBT1(char *pre,char *in,int n)
/*pre存放先序序列,in存放中序序列,n为二叉树节点个数,
本算法执行后返回构造的二叉链的根节点指针*/
{
BTNode *s;
char *p;
int k;
if (n<=0) return NULL;
s=(BTNode *)malloc(sizeof(BTNode)); //创建二叉树节点s
s->data=*pre;
for (p=in;p<in+n;p++) //在中序序列中找等于*ppos的位置k
if (*p==*pre) //pre指向根节点
break; //在in中找到后退出循环
k=p-in; //确定根节点在in中的位置
s->lchild=CreateBT1(pre+1,in,k); //递归构造左子树
s->rchild=CreateBT1(pre+k+1,p+1,n-k-1); //递归构造右子树
return s;
}
BTNode *CreateBT2(char *post,char *in,int n)
/*post存放后序序列,in存放中序序列,n为二叉树节点个数,
本算法执行后返回构造的二叉链的根节点指针*/
{
BTNode *s;
char r,*p;
int k;
if (n<=0) return NULL;
r=*(post+n-1); //根节点值
s=(BTNode *)malloc(sizeof(BTNode)); //创建二叉树节点s
s->data=r;
for (p=in;p<in+n;p++) //在in中查找根节点
if (*p==r)
break;
k=p-in; //k为根节点在in中的下标
s->lchild=CreateBT2(post,in,k); //递归构造左子树
s->rchild=CreateBT2(post+k,p+1,n-k-1); //递归构造右子树
return s;
}
int main()
{
ElemType pre[]="ABDGCEF",in[]="DGBAECF",post[]="GDBEFCA";
BTNode *b1,*b2;
b1=CreateBT1(pre,in,7);
printf("b1:");DispBTree(b1);printf("\n");
b2=CreateBT2(post,in,7);
printf("b2:");DispBTree(b2);printf("\n");
DestroyBTree(b1);
DestroyBTree(b2);
return 1;
}
头文件btree.h:
//二叉树的基本运算算法
#include <stdio.h>
#include <malloc.h>
#define MaxSize 100
typedef char ElemType;
typedef struct node
{
ElemType data; //数据元素
struct node *lchild; //指向左孩子节点
struct node *rchild; //指向右孩子节点
} BTNode;
void CreateBTree(BTNode * &b,char *str) //创建二叉树
{
BTNode *St[MaxSize],*p=NULL;
int top=-1,k,j=0;
char ch;
b=NULL; //建立的二叉树初始时为空
ch=str[j];
while (ch!='\0') //str未扫描完时循环
{
switch(ch)
{
case '(':top++;St[top]=p;k=1; break; //为左孩子节点
case ')':top--;break;
case ',':k=2; break; //为孩子节点右节点
default:p=(BTNode *)malloc(sizeof(BTNode));
p->data=ch;p->lchild=p->rchild=NULL;
if (b==NULL) //*p为二叉树的根节点
b=p;
else //已建立二叉树根节点
{
switch(k)
{
case 1:St[top]->lchild=p;break;
case 2:St[top]->rchild=p;break;
}
}
}
j++;
ch=str[j];
}
}
void DestroyBTree(BTNode *&b)
{ if (b!=NULL)
{ DestroyBTree(b->lchild);
DestroyBTree(b->rchild);
free(b);
}
}
BTNode *FindNode(BTNode *b,ElemType x)
{
BTNode *p;
if (b==NULL)
return NULL;
else if (b->data==x)
return b;
else
{
p=FindNode(b->lchild,x);
if (p!=NULL)
return p;
else
return FindNode(b->rchild,x);
}
}
BTNode *LchildNode(BTNode *p)
{
return p->lchild;
}
BTNode *RchildNode(BTNode *p)
{
return p->rchild;
}
int BTHeight(BTNode *b)
{
int lchildh,rchildh;
if (b==NULL) return(0); //空树的高度为0
else
{
lchildh=BTHeight(b->lchild); //求左子树的高度为lchildh
rchildh=BTHeight(b->rchild); //求右子树的高度为rchildh
return (lchildh>rchildh)? (lchildh+1):(rchildh+1);
}
}
void DispBTree(BTNode *b)
{
if (b!=NULL)
{ printf("%c",b->data);
if (b->lchild!=NULL || b->rchild!=NULL)
{ printf("("); //有孩子节点时才输出(
DispBTree(b->lchild); //递归处理左子树
if (b->rchild!=NULL) printf(","); //有右孩子节点时才输出,
DispBTree(b->rchild); //递归处理右子树
printf(")"); //有孩子节点时才输出)
}
}
}
/*以下主函数用做调试
void main()
{
BTNode *b;
CreateBTree(b,"A(B(D,E),C(,F))");
DispBTree(b);
printf("\n");
}
*/
4. 测试
|




 苏公网安备 32061202001004号
苏公网安备 32061202001004号



